Most people know how to calculate the percentage of a given amount or number. But did you know there’s a method to find the average of several percentages? This is called the average percentage formula.
In this article, we’ll delve into the basics of percentages, show you how to calculate them, and explain how to find average percentages using practical examples. This guide aligns with O Level & IGCSE Mathematics standards, ensuring a clear and educational approach.
In this article, we’ll delve into the basics of percentages, show you how to calculate them, and explain how to find average percentages using practical examples. This guide aligns with O Level & IGCSE Mathematics standards, ensuring a clear and educational approach.
In simple terms, percentages are portions of something out of 100, a concept frequently covered in O Level & IGCSE Mathematics.
How Are Percentages Calculated?
Example:
Imagine you are running a survey to understand customer satisfaction. Out of 200 responses, 150 people rated their satisfaction as “excellent.” To calculate the percentage of satisfied customers, you would use the following formula:
This means 75% of the respondents are highly satisfied with your service.
Calculating percentages helps put into perspective how much of a certain amount is being used or considered. In the real world, percentages represent various things such as taxes, survey results, and more. They help attach meaning to these figures.
Want to master percentages and other math concepts?
Book a 1-on-1 session now!
How to Calculate Average Percentage?
To find the average percentage, follow these straightforward steps:
- Sum of Individual Percentages: Add together all the individual percentages.
- Count of Percentages: Count the total number of percentages.
- Divide the Sum by the Count: Divide the sum of the percentages by the number of percentages.
Here’s the formula for calculating the average percentage:
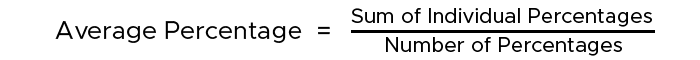
Additional Steps You May Consider
When calculating average percentages, sometimes additional steps are necessary to ensure accuracy, especially in more complex scenarios. Here’s a more detailed approach commonly taught in O Level & IGCSE Mathematics:
Step 1: Convert Percentages into Decimals
Convert each percentage to a decimal by dividing by 100. For example, 80% becomes 0.80.
Here are more examples:
– 67% becomes 0.67.
– 23% becomes 0.23.
Step 2: Determine the Number That Each Decimal Represents
Multiply each decimal by the total amount it represents. For example
– If 67% of 150 is to be calculated, then (0.67×150=100.5).
– If 23% of 350 is to be calculated, then (0.23×350=80.5).
Step 3: Add Both Numbers and Sample Size Totals
Sum the numbers obtained in Step 2 and add the total amounts they represent:
– Sum of the numbers: (100.5 + 80.5 = 181).
– Sum of the sample sizes: (150 + 350 = 500).
Step 4: Calculate the Percentage Average
Divide the sum of the numbers by the total sample size, then multiply by 100 to convert back to a percentage:
Struggling with math concepts? Get personalized assistance with our 1-on-1 tutoring sessions!
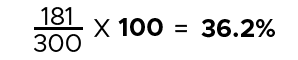
Calculating the Average Percentage Using a Real-Life Example
Let’s consider you have three products with the following customer satisfaction rates and number of respondents:
– Product A: 85% satisfaction (200 respondents)
– Product B: 75% satisfaction (150 respondents)
– Product C: 90% satisfaction (250 respondents)
– Product A: 85% satisfaction (200 respondents)
– Product B: 75% satisfaction (150 respondents)
– Product C: 90% satisfaction (250 respondents)
Step 1: Convert Percentages into Decimals
Convert each percentage to a decimal:
85% = 0.85
75% = 0.75
90% = 0.90
Step 2: Determine the Number That Each Decimal Represents
Multiply each decimal by the number of respondents:
[ 0.85 x 200 = 170 ]
[ 0.75 x 150 = 112.5 ]
[ 0.90 x250 = 225 ]
Step 3: Add Both Numbers and Sample Size Totals
Sum of the satisfaction numbers:
[ 170 + 112.5 + 225 = 507.5 ]
Sum of the total respondents:
[ 200 + 150 + 250 = 600 ]
Step 4: Calculate the Percentage Average
Divide the sum of the satisfaction numbers by the total number of respondents and multiply by 100:
So, the average customer satisfaction rate across the three products is approximately 84.58%.
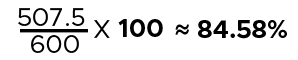
Lets Calculate Reverse Percantage
Reverse percentages are also a crucial topic in O Level & IGCSE Mathematics. They involve finding the original number before a percentage increase or decrease was applied. This is particularly useful in various real-world scenarios such as calculating the original price before tax or discount.
Example:
Suppose an item costs $120 after a 20% increase. To find the original price, we can use the reverse percentage formula.
1-Convert the percentage to a decimal: 20% = 0.20.
2- Add 1 to the decimal: 1 + 0.20 = 1.20.
3-Divide the final amount by this sum: 1201.20=100\frac{120}{1.20} = 1001.20120=100.
So, the original price of the item was $100.